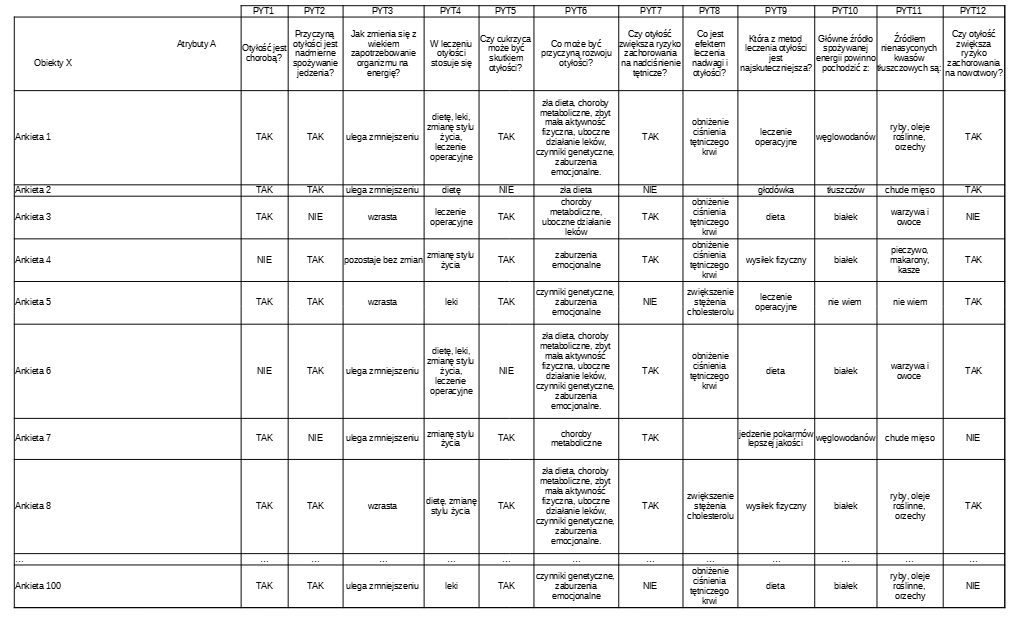
Poprzednio zajęliśmy się tematem funkcji informacji i kartoteki wyszukiwawczej.
Teraz nadszedł czas określenia czy nasz system jest kompletny i selektywny. Aby odpowiedzieć na to pytanie należałoby wpierw określić co to znaczy system kompletny, a co oznacza system selektywny. Zanim dojdziemy do tych definicji, kilka przypomnień z wykładu.
Informacją w systemie S o obiekcie x ∈ X jest zatem funkcja ρx : A →V, taka, że ρx(a) = ρ(x, a) dla każdego a ∈ A.
Parę (a,v), gdzie: a ∈A , v ∈Va nazywać będziemy deskryptorem. W naszym przykładzie to np.: (PYT1,TAK), (PYT9,”dieta”), (PYT9,”wysiłek fizyczny”) itp. Zbiór deskryptorów wyznaczony przez informację o obiekcie x to opis obiektu x. Kolejność deskryptorów w zasadzie nie jest istotna.
- Informacją w systemie S będziemy nazywać każdą funkcję ρ o argumentach w zbiorze atrybutów A oraz wartościach należących do zbioru V, taką, że ρ(a) ∈Va.
- Jeśli wszystkie zbiory X, A i V są skończone, to w każdym systemie może być tylko skończona liczba różnych informacji.
- Liczba wszystkich możliwych (różnych) informacji w systemie jest oczywiście równa: \underset{a \in A}{\sqcap} card(V_a) 1\underset{a \in A}{\sqcap} – znaczy dla każdego podzbioru; podobne do {\forall} – znaczy dla każdego, a w rezultacie chodzi o: wszystkie
anależące do zbioruA2 card(V) – funkcja kardynalna (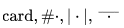
) – moc zbioru (ilość elementów zbioru).
Przykład: Nasz system S ma 12 atrybutów PYT1, PYT2, PYT5, PYT7, PYT12 z 2 wartościami oraz PYT3 z 3 wartościami, PYT10 z 4 wartościami i PYT9 z 5 wartościami, i te wyliczamy jako iloczyn możliwych wartości 2*2*2*2*2*3*4*5 (to jeszcze nie koniec!),
ale w przypadku PYT4, PYT6, PYT8 i PYT11 sprawa jest bardziej skomplikowana, bowiem są to pytania posiadające możliwość posiadania wartości złożonej, gdzie: - Każda informacja ρ wyznacza pewien zbiór obiektów Xρ takich, że Xρ = {x ∈X : ρx = ρ}, a więc obiektów mających w systemie jednakową informację (opis) – czyli są nierozróżnialne.
- Gdy danej informacji nie odpowiada żaden obiekt mówimy, że informacja jest pusta i zapisujemy jako Xρ = ∅. W przeciwnym przypadku mówimy, że informacja jest niepusta.
System jest kompletny wtedy i tylko wtedy gdy każda informacja jest niepusta (czyli gdy każdej informacji odpowiada co najmniej jeden obiekt).
Patrząc na powyższą definicję okazuje się, że systemem kompletnym dla naszej ankiety byłby system złożony z 503316480 obiektów o unikalnych opisach obiektów x.
System jest selektywny wtedy i tylko wtedy gdy każdej informacji odpowiada co najwyżej jeden obiekt.np. system informacji bibliotecznej jest na ogół nieselektywny, zaś informacji o pojazdach (niepowtarzalny VIN i numer rejestracyjny) selektywny.
Nasz system byłby selektywny, jeśli posiadałby nie więcej jak 503316480 unikalnych opisów obiektów x.
Powiemy, że obiekty xn ,xm ∈X są nierozróżnialne w systemie S ze względu na atrybut a ∈A wtedy i tylko wtedy, gdy:
\Large \rho_{x_n}(a) = \rho_{x_m}(a)
Nierozróżnialność obiektów xn i xm ze względu na atrybut a będziemy zapisywać jako: x_n \, \overset{\sim}{a} \, x_m.
Możliwe jest także takie zdarzenie, że dwa obiekty w systemie S mają identyczne deskryptory dla każdego atrybutu, wtedy mówimy, że takie obiekty są nierozróżnialne w systemie S.
\Large x_n \, \overset{\sim}{S} \, x_m \Leftrightarrow \underset{a \in A}{\forall} ( \rho_{x_n}(a) = \rho_{x_m}(a) ) \Leftrightarrow \rho_{x_n} = \rho_{x_m}
Uwaga: Odrobina przypomnienia z matematyki i kwantyfikatorów w odnośniku: 3Kwantyfikator ogólny (duży):
\underset{a \in A}{\sqcap} – dla każdego podzbioru a należącego do zbioru A;
\underset{a \in A}{\forall} dla wszystkich a należącego do zbioru A;
\underset{a \in A}{\bigwedge} dla każdego a należącego do zbioru A
Wszystkie powyższe zapisy znaczą w zasadzie to samo. Warto zapoznać się z Kwantyfikatorem egzystencjalnym oraz wynikiem stosowania negacji obu. 4Przydatne są i… spotkamy jeszcze inne kwantyfikatory ich wyjaśnienie możemy znaleźć choćby tutaj .
Zadanie 1
Określ warunek kompletności dla systemu zaproponowanego przez Ciebie.
Zadanie 2
Sprawdź, czy Twój system jest kompletny i selektywny – podaj przykłady na potwierdzenie, lub zaprzeczenie tych tez.
Zadanie 3
Znajdź obiekty nierozróżnialne w systemie i podaj ich przykłady
Znajdź obiekty nierozróżnialne ze względu na wybrany atrybut i podaj ich przykłady
Zadanie 4
Mając dany system S, określ i uzasadnij czy tak podany system jest kompletny i selektywny:
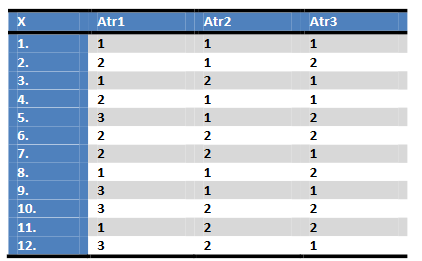
V_{atr1} = \{1,2,3\} ; V_{atr2} = \{1,2\}; V_{atr3} = \{1,2\}