Metoda ta umożliwia uzyskanie bardzo krótkich czasów odpowiedzi dla zapytań z pewnej klasy. Jest metodą często wykorzystywaną w systemach wyszukiwania informacji.
W zadanym systemie S, przy zbiorze obiektów X opisanych atrybutami A, posiadającymi wartości V z funkcją informacji \rho obiekty systemu opisane są iloczynem niezaprzeczonych deskryptorów. Opisy obiektów t_x umieszczone są w systemie S w dowolny sposób, każdy posiadając przypisany mu adres. Zatem, można wyróżnić adresy obiektów x_1, x_2, x_3, ..., x_n będące odpowiednio n_1, n_2, n_3, ..., n_m wykorzystując funkcję adresującą \mu w sposób:
\mu:X \rightarrow N, przy czym \mu(x) = \mu(y) \iff t_x = t_y
co oznacza, że obiekty o tym samym opisie deskryptorowym otrzymują ten sam adres.
Dla wszystkich deskryptorów w systemie tworzymy listy adresów obiektów, grupując je po identycznym deskryptorze d_i(d_i \in t_x) są to listy inwersyjne i oznaczamy je \alpha(d_i)
\alpha(d_i) = \{ n_1, \dots, n_z \}, gdzie
d_i = (a_i, v_i), a_i \in A, v_i \in V_{a_i}
Zależnie od organizacji implementacyjnej w listach inwersyjnych występują bezpośrednio obiekty lub wskaźniki na obiekty.
Spis treści
Wyszukiwanie w systemie
Pytania do systemu S zadawane są w postaci termu t będącego sumą termów składowych t = t_1 + t_2 + ... + t_m.
W zależności czy termy składowe są postaci prostej (pojedynczej), czy złożonej (iloczynu deskryptorów) możemy wyróżnić dwie drogi uzyskania odpowiedzi z systemu.
Termy składowe proste
Pytanie do systemu jest przedstawiane jako suma deskryptorów:
t = d_1 + d_2 + ... +d_k
Odpowiedzią na pytanie t jest suma list inwersyjnych wygenerowanych dla jego termów składowych, tak więc:
\sigma(t) = \alpha(d_1) \cup \alpha(d_2) \cup ... \cup \alpha(d_k)
Termy składowe złożone
W przypadku termów złożonych zawierających termy składowe w postaci iloczynu deskryptorów odpowiedzią jest sumą odpowiedzi na termy składowe, a odpowiedzią na termy składowe jest część wspólna (przecięcie) list inwersyjnych występujących w pytaniu t_i .
\sigma(t) = \sigma(t_1) \cup \sigma(t_2) \cup ... \cup \sigma(t_k) , gdzie:
\sigma(t_i) = \alpha(d_1) \cap \alpha(d_2) \cap ... \cap \alpha(d_k) \Leftrightarrow t_i = d_1 \cdot d_2 \cdot ... \cdot d_k
Teraz należy odnieść się do konkretnych obiektów (lub je znaleźć jeśli były wskazywane przez adres) i dokonać ekstrakcji odpowiedzi na pytanie t = t_1 + t_2 + ... +t_m , gdzie \sigma(t) = \sigma(t_1) \cup \sigma(t_2) \cup ... \cup \sigma(t_m) z założeniem, że:
\sigma(t_i) = \{ x \in X, \mu(x) = n_i \Leftrightarrow n_i \in N` = \underset{j}{\bigcap} \mu(d_j)\}, gdzie:
N` \subseteq N, \hspace{5mm} d_j \in t_i
Znaczy to, że odpowiedź na pytanie t jest sumą odpowiedzi na pytania składowe, przy czym odpowiedzią na pytanie składowej jest przecięcie zbiorów obiektów reprezentowanych za pomocą list inwersyjnych które to są powiązane z deskryptorami występującymi w pytaniu składowym.
Redundancja
Jak widać z powyższego opisu metoda list inwersyjnych wnosi dużą redundancję z powodu często wielokrotnego występowania obiektów (bądź wskaźników do nich) w listach inwersyjnych. Redundancja ta wygląda wg wzoru:
\Large R = \frac{ \sum\limits_{i=1}^r \overline{\overline{\alpha(d_i)}} - N }{N} , gdzie:
- r – liczba deskryptorów w systemie,
- N – liczba obiektów (lub wskaźników na obiekt).
Przykład użycia
Odnosząc się do naszego przykładu bazy danych możemy przeprowadzić jej transkrypcję do MLI tworząc po kolei listy inwersyjne. Dla uproszczenia implementacyjnego zakładamy, że w listach tych występują od razu obiekty1a nie wskaźniki na nie, chociaż w przypadku większych systemów właściwe jest użycie wskaźników.
- \alpha( M ) = \{ x_1, x_4, x_ 5, x_6, x_8, x_{10}, x_{13}, x_{15}, x_{16}, x_{17}, x_{18} \} – wszyscy mężczyźni,
- \alpha( K ) = \{ x_2, x_3, x_ 7, x_9, x_{11}, x_{12}, x_{14}, x_{19}, x_{20} \} – wszystkie kobiety,
- \alpha( a ) = \{ x_4 \} – wiek poniżej 20 lat,
- \alpha( b ) = \{ x_1, x_3, x_ 5, x_9, x_{10}, x_{11}, x_{12}, x_{13}, x_{14}, x_{18}, x_{19}, x_{20}\} – wiek 20 ÷ 35 lat,
- \alpha( c ) = \{ x_2, x_ 6, x_7, x_8, x_{15}, x_{16}, x_{17} \} – wiek > 35 lat,
- \alpha( P ) = \{ x_3 \} – wykształcenie podstawowe,
- \alpha( S ) = \{ x_2, x_4, x_{12}, x_{13} \} – wykształcenie średnie,
- \alpha( W ) = \{ x_1, x_5, x_ 6, x_7, x_8, x_9, x_{10}, x_{11}, x_{14}, x_{15}, x_{16}, x_{17}, x_{18}, x_{19}, x_{20} \} – wykształcenie wyższe,
- \alpha( D ) = \{ x_1, x_5, x_ 6, x_7, x_8, x_9, x_{10}, x_{11}, x_{14}, x_{15}, x_{16}, x_{17}, x_{18}, x_{19}, x_{20} \} – praca jako dydaktyk,
- \alpha( T ) = \{ x_4, x_{12}, x_{13} \} – praca jako technik,
- \alpha( A ) = \{ x_2, x_3 \} – praca administracyjna,
- \alpha( BT ) = \{ x_2, x_3, x_4, x_{12}, x_{13} \} – tytuł licencjata,
- \alpha( MR ) = \{ x_5, x_{10}, x_{19} \} – tytuł magistra,
- \alpha( DR ) = \{ x_6, x_7, x_9, x_{11}, x_{14}, x_{18}, x_{20} \} – tytuł doktora,
- \alpha( DC ) = \{ x_8, x_{15}, x_{16} \} – tytuł doktora habilitowanego,
- \alpha( PR ) = \{ x_1, x_{17} \} – tytuł profesora.
Zaczerpnijmy pytania z poprzednich przykładów i zadajmy do systemu następujące pytanie:
t_1 = (A_4, D) \cdot (A_2, b)aby znaleźć odpowiedź, musimy sięgnąć do list inwersyjnych odpowiadających odpowiednim deskryptorom czyli [9] i [4]. Rozpisując to mamy następująca postać:
\sigma(t_1) = \alpha(D) \cap \alpha(b) , czyli
\sigma(t_1) = \{ x_1, x_5, x_ 6, x_7, x_8, x_9, x_{10}, x_{11}, x_{14}, x_{15}, x_{16}, x_{17}, x_{18}, x_{19}, x_{20} \} \\ \cap \\ \{ x_1, x_3, x_ 5, x_9, x_{10}, x_{11}, x_{12}, x_{13}, x_{14}, x_{18}, x_{19}, x_{20} \}
daje nam to odpowiedź postaci:
\sigma(t_1) = \{ x_1, x_5, x_9, x_{10}, x_{11}, x_{14}, x_{18}, x_{19}, x_{20} \}
Bardziej skomplikowane2ale tylko ze względu na mnogość dokonywanych operacji, nie ich skomplikowanie będzie szukanie odpowiedzi na drugie pytanie z przykładu:
t_2 = (A_2, b) \cdot (A_4, T) + (A_3, S) \cdot ( \neg (A_4, A))
W tym przypadku ponownie musimy rozpisać pytanie na pytania składowe z wykorzystaniem dopełnienia przy użytej negacji, a więc:
t_2 = (A_2, b) \cdot (A_4, T) + (A_3, S) \cdot ( (A_4, T) + (A_4, D) )
⇓
t_2 = (A_2, b) \cdot (A_4, T) + (A_3, S) \cdot (A_4, T) + (A_3, S) \cdot (A_4, D)
Zajmując się każdym powstałym t_2^1, t_2^2 i t_2^3termem składowym z osobna, szukamy sumy zbiorów odpowiedzi na takie pytanie, a więc:
\sigma(t_2) = \sigma(t_2^1) \cup \sigma(t_2^2) \cup \sigma(t_2^3)Analogicznie do pierwszego przykładu wyznaczamy odpowiedzi w tych trzech wariantach, i tak:
- \sigma(t_2^1) = \alpha(b) \cap \alpha(T)
- \sigma(t_2^2) = \alpha(S) \cap \alpha(T)
- \sigma(t_2^3) = \alpha(S) \cap \alpha(D)
otrzymujemy:
Term składowy pierwszy:
\sigma(t_2^1) = \{ x_1, x_3, x_ 5, x_9, x_{10}, x_{11}, x_{12}, x_{13}, x_{14}, x_{18}, x_{19}, x_{20}\} \\ \cap \\ \{ x_4, x_{12}, x_{13} \}
⇓
\sigma(t_2^1) = \{ x_{12}, x_{13} \}
Term składowy drugi:
\sigma(t_2^2) = \{ x_2, x_4, x_{12}, x_{13} \} \\ \cap \\ \{ x_4, x_{12}, x_{13} \}
⇓
\sigma(t_2^2) = \{ x_4, x_{12}, x_{13} \}
Term składowy trzeci:
\sigma(t_2^3) = \{ x_2, x_4, x_{12}, x_{13} \} \\ \cap \\ \{ x_1, x_5, x_ 6, x_7, x_8, x_9, x_{10}, x_{11}, x_{14}, x_{15}, x_{16}, x_{17}, x_{18}, x_{19}, x_{20} \}
⇓
\sigma(t_2^3) = \{ \varnothing \}
Odpowiedzią na nasz term jest suma odpowiedzi na termy składowe, a więc:
\sigma(t_2) = \{ x_{12}, x_{13} \} \cup \{ x_4, x_{12}, x_{13} \} \cup \{ \varnothing \}
⇓
\sigma(t_2) = \{ x_4, x_{12}, x_{13} \}
Zadania
Zadanie 1
Dany jest system informacyjny S = \{ X, A, V, \rho \}
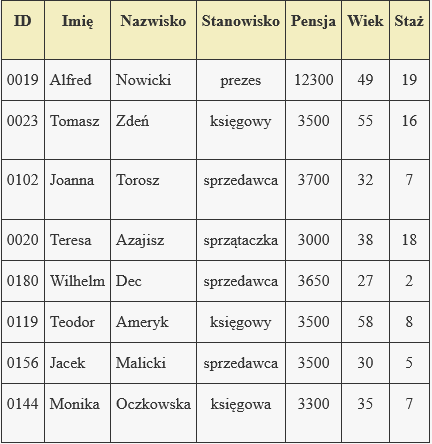
Przekształć system do metody list inwersyjnych i wyszukaj:
- wszystkie osoby mające więcej jak 10 lat stażu w firmie zarabiające poniżej 5000zł
- wszystkie osoby nie zajmujące stanowisk służb porządkowych i nie będące prezesem
Zadanie 2
Dany jest system informacyjny S. Fragment zawartych w nim opisów wygląda następująco:
\alpha(wiek, młodzież) = \{1,2,3,4,9,11,14,16,17\} \\ \alpha(wiek, dorosły) = \{5,6,12,13,18,19\} \\ \alpha(wiek, starszy) = \{7,8,10,15,20\} \\ \alpha(sport, brak)= \{1,2,3\} \\ \alpha(sport, basen) = \{9,14,16,20\} \\ \alpha(sport, rower\ i biegi) = \{4,5,6,8,10,12,17,19\} \\ \alpha(sport, wędrówki\ górskie) = \{7,11,13,15,18\} \\ \alpha(hobby, sztuka) = \{1,2,3,9\} \\ \alpha(hobby, film\ i muzyka) = \{5,6,8,11,12,13,14,15,17,18,19,20\} \\ \alpha(hobby, książka) = \{4,7,10,16\}
a) Ile opisanych jest tu obiektów ? Podaj opisy tych obiektów.
b) Oblicz redundancję w tym systemie.