Metoda List Prostych

Jest to najprostsza z metod wyszukiwania zwana również metodą przeglądu zupełnego. Zakładamy, że dany jest system S, będący zbiorem obiektów X, opisanych atrybutami należącymi do A i posiadającymi wartości w zbiorze V, a system opisuje funkcja informacji \rho . W tej metodzie informacje o obiektach są nieuporządkowane i mogą wynikać np. z kolejności napływania danych do systemu. Informacja \rho_x jest funkcją opisującą dany obiekt x, przyporządkowującą każdemu atrybutowi a obiektu x jego wartość v tworzącą term w języku informacyjnym L_s w postaci t_x.

t_x=(a_1, v_1) \cdot (a_2, v_2) \cdot ... \cdot (a_n, v_n), (a_i \in A, v_i \in V_{a_i}), n – liczba atrybutów systemu

Term t_x to opis obiektu x w języku L_s. Opisy te w metodzie list prostych mogą być pamiętane w dowolnej kolejności. W zależności od przyjętego L_s ta sama informacja może być zapamiętana w różny sposób.

Można zauważyć, że jeżeli t_i jest założonym termem składowym, a t_x jest opisem obiektu x w systemie S to zachodzi t_i = t_x wtedy i tylko wtedy, gdy w opisie obiektu x i w termie składowym t_i występują te same deskryptory.

\underset{d_i \in 1..m}\bigwedge d_i=d_j\Longleftrightarrow

Jeżeli zaś w opisie obiektu x występują co najmniej deskryptory termu składowego t_i, to taki term zawiera się w termie t_x i zachodzi zależność:

t_i \leq t_x.

Pytania do systemu S zadawane są w postaci termów t, które mają postać sumy termów składowych:

t = t_1 + t_2 + ... + t_m,

gdzie t_i jest termem składowym, gdzie i \in (1..m).

Przyjmijmy istnienie systemu zawierającego opisy ludzi w postaci wieku, koloru oczu, wzrostu, płci itp. Zapytanie do takiego systemu może wyglądać następująco:

t=(wiek, 22) \cdot (kolor oczu, szare) + (kolor oczu, niebieskie) \cdot (wzrost, 180) \cdot (wiek,23) \cdot (płeć, mężczyzna).

Wyszukiwanie w metodzie list prostych może zostać zrealizowane na dwa sposoby.

Sposób I

Przeglądamy kolejne opisy obiektów i selekcjonujemy te, które w swym opisie zawierają term składowy t_i pytania, gdzie i \in {1 .. m}.

Odpowiedź na taki term składowy t_i jest następująca:

\sigma(t_i) = { x \in X, t_i \leq t_x }, gdzie:

• t_x – opis obiektu x w systemie S,
• t_i – term składowy pytania.

Zbiór obiektów będący sumą odpowiedzi na termy składowe jest odpowiedzią na pytanie t.

\sigma(t) = \sigma(t_1) \cup \sigma(t_2) \cup ... \cup \sigma(t_m)

Rozpatrując poniższy przykład mamy wyjaśnione wyszukiwanie wg tego sposobu.

Niech obiekty x_1, x_2, x_3 będą odpowiednio miały następujące opisy:

• t_{x_1} = (wiek, 33) \cdot (płeć, kobieta) \cdot (kolor oczu, niebieski) \cdot (wzrost,170);
• t_{x_2} = (płeć, mężczyzna) \cdot (wiek, 50) \cdot (wzrost, 182) \cdot (kolor oczu, szary);
• t_{x_3} = (wzrost, 180) \cdot (kolor oczu, czarny) \cdot (wiek, 23) \cdot (płeć, mężczyzna);

Do systemu zadajemy pytanie w postaci:

t = (wiek, 33) \cdot (płeć, kobieta) + (płeć, mężczyzna) \cdot (kolor oczu, szary)

Daje nam to termy składowe postaci:

• t_1= (wiek, 33) \cdot (płeć, kobieta)
• t_2= (płeć, mężczyzna) \cdot (kolor oczu, szary)

a cały term t= t_1 + t_2

Porównujemy pierwszy term składowy t_1, kolejno z opisami obiektów t_{x_1}, t_{x_2}, t_{x_3} i otrzymujemy:

\sigma(t_1)=\{x_1\}

Analogicznie postępujemy z drugim termem składowym t_2 i otrzymujemy

\sigma(t_2)=\{x_2\}

Zatem odpowiedzią na term t będzie suma odpowiedzi na termy składowe t_1 i t_2, czyli:

\sigma(t) = \{x_1\} \cup \{x_2\} = \{x_1, x_2\}

Sposób II

W drugim sposobie porównujemy pełne pytanie t z kolejnymi opisami obiektów i wybieramy obiekty zawierające w swoim opisie przynajmniej jeden term składowy pytania t. Zbiór wyselekcjonowanych w ten sposób obiektów x_i, gdzie x \in X jest odpowiedzią na pytanie t.

\sigma(t) = \{x \in X, \underset{t_i \in t}{\bigvee} t_i \leq t_x \}

Gdzie:

• t_x – to opis obiektu x,
• t_i – to term składowy pytania,
• t_i \in t – oznacza, że term składowy t_i występuje w pytaniu t.

Rozpatrzmy więc przykład wyszukiwania w przedstawiony sposób. Załóżmy system S z obiektami takimi samymi jak w poprzednim przykładzie. Wyspecyfikowane pytanie jest postaci:

t=(wiek,33) \cdot (płeć, kobieta) + (kolor oczu, szary) \cdot (płeć, mężczyzna)

Porównując całe pytanie t kolejno wpierw term składowy t_1, a potem t_2 po kolei z każdym opisem obiektów systemu S określamy, czy term składowy zawiera się w tym opisie:

t_i \leq t_{x_m}, gdzie:

• i to indeks kolejnego termu składowego,
• m to indeks kolejnego obiektu x w systemie S

Jeśli się zawiera, to taki obiekt jest odpowiedzią na pytanie t. Reasumując stwierdziliśmy w naszym przykładzie, że:

t_1 \leq t_{x1}, t_2 \leq t_{x_2}, a t_1 \nleq t_{x_3}, i t_2 \nleq t_{x_3}

Odpowiedź będzie zatem miała postać:

\sigma(t) = \{ x_1, x_2 \}

Złożoność obliczeniowa

Łatwo zauważyć, że w przypadku sposobu pierwszego aby znaleźć odpowiedź na pytanie należy wykonać m-krotnego przeglądu wszystkich opisów w bazie danych, gdzie m to liczba termów składowych. Średni czas wyszukiwania wynosi zatem:

\tau = N \cdot m \cdot \tau_0 , gdzie:

• N – liczba opisów obiektów w bazie,
• m – liczba termów składowych w pytaniu t,
• \tau_0 – średni czas przeglądu jednego opisu obiektu.

Drugi sposób dokonuje jednokrotnego przeglądu opisów obiektów w bazie, zatem:

\tau = N \cdot \tau_0^`, gdzie:

• \tau_0^` – średni czas przeglądu jednego opisu w drugim przypadku. Trzeba jednak pamiętać, ze samo sprawdzenie opisu jest bardziej złożone bowiem sprawdzamy od razu w tym przebiegu wszystkie termy składowe, czyli czas przeglądu jednego dokumentu może być w tym przypadku znacznie dłuższy.

Zadanie

Dany jest system S zgodny z poniższą definicją:

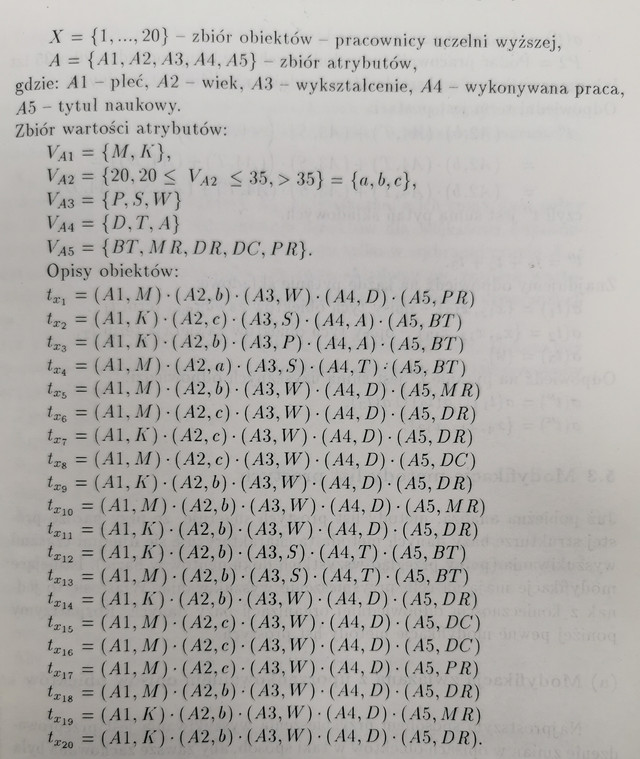
Pytanie 1: Podać osoby będące pracownikami dydaktycznymi w wieku powyżej 35 lat.

Pytanie możemy zapisać w postaci termu:

t^` = (A4,D) \cdot (A2,c)

Pytanie 2: Podać pracowników technicznych w wieku pomiędzy 20 a 35 lat lub pracowników z wykształceniem średnim nie administracyjnych.

Takie pytanie możemy zapisać:

t^{``} = (A2,b) \cdot (A4, T) + (A3, S) \cdot (\neg(A4,A)) =

= (A2, b) \cdot (A4, T) + (A3, S) \cdot ((A4,T) + (A4, D)) =

= (A2, b) \cdot (A4, T) + (A3, S) \cdot (A4,T) + (A3, S) \cdot (A4, D)

Pytanie 3: Rozpisz i odszukaj: Pracowników dydaktycznych, którzy mają tytuł naukowy poniżej doktora; pracowników administracyjnych i technicznych z wykształceniem poniżej magistra.

Pytanie 4: Rozpisz i odszukaj: Kobiety z tytułem naukowym profesora, które mają powyżej 35 lat oraz wszystkie kobiety z tytułem naukowym doktora w średniej kategorii wiekowej.