Metoda Saltona nie jest metodą podobną do poprzednich. Jej pierwotną destynacją jest przetwarzanie angielskiego języka naturalnego. Z tego względu nie jest prostą metodą do implementacji, a różnice lingwistyczne pomiędzy językami stanowią dodatkową trudność adaptacyjną.
Dla zrozumienia tej metody porzucimy język naturalny dla języka deskryptorowego, którego używaliśmy dotychczas. Podobnie jak poprzednio mamy do czynienia z systemem informacyjnym opartym na czwórce:
< X, A, V, \rho >
Opisy obiektów znajdujących się w bazie danych pogrupowane są w zbiory:
X_i, \quad (i = 1, .., m),
a zbiory spełniają warunek:
X = \bigcup\limits_{i}^{m} X_i
Każdy taki zbiór (grupa obiektów) X_i poprzedzona jest identyfikatorem grupy zwanym centroidem C_i lub profilem P_1 .
X_i = ( C_i, \{t_{x_i}\} )
W celu grupowania obiektów wykorzystuje się dedykowane metody, z których dwie (Rocchia i Doyle’a) zostały przedstawione w dalszej części.
Spis treści
Wyszukiwanie w systemie
Wyszukiwanie w systemie informacyjnym zorganizowanym wg metody Saltona odbywa się poprzez znalezienie odpowiedzi przybliżonej do zadanego do systemu termu t :
\sigma(t_j) \approx X_j = \{ X_i \subseteq X, \quad t_j \leq C_i \}, \quad gdzie \quad X_i = ( C_i, \{ t_{x_i} \} )
a następnie na przeglądzie zupełnym zlokalizowanej w ten sposób grupy:
\sigma(t_j) = \{ x_i \in X_j, \quad t_j \leq t_{x_i} \}
Jeśli w procesie grupowania pozostały obiekty, których nie udało się przyporządkować do żadnego zbioru to koniecznym jest dokonanie wyszukiwania przeglądem zupełnym wśród “grupy” takich obiektów.
Przy dużej bazie danych możliwe jest także dalsze jej strukturyzowanie poprzez grupowanie centroidów, co tworzy struktury drzewiaste (Pnie i gałęzie prowadzące do opisów obiektów). Wyszukiwanie w takiej strukturze odbywa się poprzez selekcję pni grupy o opisie jak najbardziej zbliżonym do t_j , a następnie w ramach tych gałęzi odszukujemy grupy obiektów poprzez porównanie wektorów centroidów z termem składowym. Na końcu wyselekcjonowane grupy przeszukujemy przeglądem zupełnym.
Algorytmy grupowania obiektów
Algorytm Roccia
W algorytmie Roccia dyskryminatorem przynależności do grupy jest podobieństwo p obiektu centralnego x_c z elementami x_i \in X . Taki współczynnik podobieństwa można wyliczyć ze wzoru [1]:
p = \Large{ \frac{ \aleph \{ d_{x_i} \cap d_{x_c} \} }{ \aleph \{ d_{x_c} \} }}
gdzie:
- \aleph (czyt: alef) – to funkcja card()1liczba kardynalna zbioru, czyli moc zbioru,
- d_{x_i} – zbiór deskryptorów w opisie obiektu x_i ,
- d_{x_c} – zbiór deskryptorów w opisie obiektu centroidalnego x_c .
Wybrany obiekt x_c poddajemy testowi gęstości. Za publikacją prof. Wakulicz-Deji2Podstawy Metod Wyszukiwania Informacji. Analiza Metod. Akademicka Oficyna Wydawnicza PLJ, Warszawa 1995. zakładamy:
«Niech N_1, N_2, p_1, p_2 będą założonymi parametrami metody. N_1, N_2 – założone rozmiary grupy (liczba obiektów w grupie), przy czym N_1 > N_2 ; p_1, p_2 – założone współczynniki podobieństwa, przy czym p_2 > p_1 . Powiemy, że obiekt x_c spełnia test gęstości, jeżeli co najmniej N_1 obiektów ma z wybranym obiektem centralnym x_c współczynnik podobieństwa większy od p_1 , a co najmniej N_2 obiektów większy o p_2 . Fakt, czy dany obiekt x_c spełnia test gęstości, zależy od doboru parametrów N_1, N_2, p_1, p_2 . Wybór tych parametrów jest albo ustalony w systemie ze względu na jego założenia, albo ustalony na drodze eksperymentu.»
Dla obiektu, spełniającego test gęstości wyznacza się współczynnik progowy p_{min} . Wszystkie obiekty szeregujemy w kolejności malejącej wyznaczonego dla nich współczynnika podobieństwa do x_c . Należy wyróżnić zbiór minimalny obiektów, których współczynnik podobieństwa z obiektem centralnym x_c \geq p_2 oraz zbiór maksymalny obiektów o współczynniku podobieństwa x_c \geq p_1 . Liczbę obiektów, które znalazły się w wydzielonych zbiorach oznaczamy odpowiednio M_1, (M_1 \geq N2) oraz M_2, (M_2 \geq N_1) . Dla grupy maksymalnej M_2 obliczamy różnice pomiędzy współczynnikami podobieństwa obiektów sąsiednich. Znajdujemy współczynnik p dla obiektu x^* dla którego nastąpiła maksymalna różnica współczynników podobieństwa do obiektu x_c .
Współczynnik podobieństwa minimalny p_{min} wyznaczamy ze wzoru [2]:
p_{min} = \left\{ \begin{matrix} p_1 & - & \begin{matrix} jeżeli\ co\ najmniej\ M_1\ obiektów \\ ma\ współczynnik\ korelacji \geq p_1 \end{matrix} \\ \\ p & - & \begin{matrix} jeżeli\ więcej\ obiektów\ niż\ M_1\\ ma\ współczynnik\ podobieństwa \geq p_1 \end{matrix} \end{matrix} \right.
Jeżeli największa różnica pomiędzy współczynnikami podobieństwa sąsiednich obiektów z x_c nastąpiła wielokrotnie, to za p przyjmujemy współczynnik podobieństwa najbliższy centrum, czyli największy z możliwych.
Tworzymy centroid, czyli wektor centroidalny jako iloczyn deskryptorów występujących w opisach obiektów grupy minimalnej (M_1) . Grupę tworzą obiekty o współczynnikach podobieństwa z x_c \geq p_{min}.
Centroid traktujemy jako centrum i ponownie obliczamy współczynniki podobieństwa obiektów z wektorem. Wybieramy p_{min} i tworzymy poprawioną grupę X_1 . Algorytm powtarzamy dla zbioru X po usunięciu z niego obiektów ze zbioru X_1 tworząc grupę X_2 . Kroki powtarzamy usuwając z X po kolei sumę wszystkich wydzielonych grup X_1 \cup X_2 \cup ... aż do wyczerpania obiektów do grupowania. Należy pamiętać, że w zbiorze X mogą znajdować się nieprzyporządkowane obiekty, które tworzą ostatnią grupę i w procesie wyszukiwania należy dokonać ich przeglądu zupełnego.
Algorytm Doyle’a
Jako materiał na III zajęcia.
W algorytmie Doyle tworzymy profile wydzielonych z bazy danych grup. Bazę dzielimy na m grup. Określamy z góry zadaną wartość bazową b . Każda j-ta grupa składa się z: X_j – zbiór obiektów tej grupy, D_j – zbiór deskryptorów znajdujących się w opisach obiektów tej grupy, F_j – wektor częstości określający dla każdego deskryptora liczbę jego wystąpień w opisach obiektów. Deskryptor występujący najwięcej razy otrzymuję rangę 1, a następne odpowiednio 2, 3,… itd. Następnie obliczamy tzw. wartości pozycyjne jako różnicę pomiędzy wartością bazową b , a każdym deskryptorem d_i|_{_j} \in D_j w X_j . Otrzymane wartości stanowią profil grupy P_j składający się z wartości pozycyjnych d_i|_{_j} \in D_j. Mamy więc zbiór obiektów X_j , zbiór deskryptorów D_j oraz profil złożony z wartości pozycyjnych.
Każdemu deskryptorowu w opisie obiektu x_i \in X przyporządkowujemy wartości pozycyjne z każdej grupy o profilu P_j w której występuje opis obiektu x_i . Suma wartości pozycyjnych dla danego obiektu x_i i profilu P_j stanowi funkcję punktującą oznaczaną jako: g(x_i, Pj). Funkcja obliczana jest dla każdego x_i i każdego profilu P_j.
Nadszedł czas by w drugim etapie dokonać ponownie dokonać podziału na grupy obiektów zgodnie z wartościami funkcji punktujących. Tworząc grupę X_j' zaliczamy do niej wszystkie obiekty, których wartość funkcji punktującej jest większa od założonej wartości progowej T_j .
X_j' = \{ x_i, g(x_i, P_j) \geq T_j \}
gdzie: \qquad T_j = \left \{\begin{matrix} H_j' = \alpha(H_j'-T), & dla & H_j'>T \\ T, & dla & H_j' \leq T \end{matrix} \right.
- T – założona wartość progowa funkcji punktującej dla j-tej grupy,
- H_j' = Max g(x_i, P_j) – maksymalna wartość funkcji punktującej w j-tej grupie,
- \alpha – założony współczynnik z zakresu 0 \leq \alpha \leq 1.
Algorytm ten doprowadza do powstania m+1 grup obiektów X_j', dzie nadplanowa grupa jest zbiorem obiektów swobodnych. Te próbujemy rozdzielić do kolejnych (innych niż poprzednio) grup obiektów i powtarzamy algorytm dla stworzenia nowego podziału na grupy. Iteracje kończymy, gdy dwie kolejne dają identyczny podział na grupy.
Wyszukiwanie metodą Saltona
Dany jest system studentów szkoły wyższej, zdefiniowany następująco:
Zbiór 24 obiektów: X = \{x_1, ..., x_{24} \} ,
zbiór atrybutów A = \{ PŁ, RU, US, JO, OS, MZ, RS \},
gdzie PŁ – płeć, RU – rok urodzenia, US – ukończona szkoła średnia, JO – znajomość języka obcego, OS – średnia ocen studiów, MZ – miejsce zamieszkania, RS – rodzaj stypendium.
Zbiory wartości atrybutów mogą przyjmować następujące wartości:
- V_{PŁ} = \{ K, M \} ( Kobieta/Mężczyzna ),
- V_{RU} = \{ ..., 99, 00, 01, 02, 03,... \} ( …, 1999, 2000, 2001, 2002, 2003,… ),
- V_{US} = \{ LO, LZ, TE \} (Liceum Ogólnokształcące, Liceum Zawodowe, TEchnikum),
- V_{JO} = \{ I, II, III \} (znajomość języków obcych: jednego, dwu, trzech i więcej),
- V_{OS} = \{ a, b, c, d \} (średnia ocena: a \leq 3 < b \leq 3,2 < c \leq 3.4 < d ),
- V_{MZ} = \{ DR, DS, KP \} (dom rodzinny, dom studenta, kwatera prywatna),
- V_{RS} = \{ ZW, NP, SN \} (stypendium zwykłe, nie pobiera, stypendium naukowe).
Obiekty systemu S mają następujące opisy:
t_{x_1}=(PŁ,K)\cdot (RU,01) \cdot (US,LO) \cdot (JO,III) \cdot (OS,d) \cdot (MZ,DR) \cdot (RS, NP ), t_{x_2}=(PŁ,K)\cdot (RU,03) \cdot (US,LO) \cdot (JO,II) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_3}=(PŁ,K)\cdot (RU,03) \cdot (US,LO) \cdot (JO,II) \cdot (OS,b) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_4}=(PŁ,M)\cdot (RU,02) \cdot (US,TE) \cdot (JO,III) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_5}=(PŁ,M)\cdot (RU,01) \cdot (US,LO) \cdot (JO,II) \cdot (OS,d) \cdot (MZ,DR) \cdot (RS,NP), t_{x_6}=(PŁ,K)\cdot (RU,02) \cdot (US,TE) \cdot (JO,II) \cdot (OS,a) \cdot (MZ,DR) \cdot (RS,NP), t_{x_7}=(PŁ,M)\cdot (RU,00) \cdot (US,TE) \cdot (JO,II) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_8}=(PŁ,M)\cdot (RU,01) \cdot (US,TE) \cdot (JO,II) \cdot (OS,d) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_9}=(PŁ,M)\cdot (RU,02) \cdot (US,TE) \cdot (JO,I) \cdot (OS,c) \cdot (MZ,DR) \cdot (RS,NP), t_{x_{10}}=(PŁ,M)\cdot (RU,02) \cdot (US,TE) \cdot (JO,I) \cdot (OS,c) \cdot (MZ,DR) \cdot (RS,NP), t_{x_{11}}=(PŁ,K)\cdot (RU,00) \cdot (US,LO) \cdot (JO,II) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_{12}}=(PŁ,M)\cdot (RU,00) \cdot (US,LZ) \cdot (JO,III) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_{13}}=(PŁ,K)\cdot (RU,01) \cdot (US,LO) \cdot (JO,I) \cdot (OS,a) \cdot (MZ,DR) \cdot (RS,NP), t_{x_{14}}=(PŁ,K)\cdot (RU,01) \cdot (US,LO) \cdot (JO,I) \cdot (OS,a) \cdot (MZ,DR) \cdot (RS,NP), t_{x_{15}}=(PŁ,M)\cdot (RU,00) \cdot (US,TE) \cdot (JO,I) \cdot (OS,a) \cdot (MZ,DR) \cdot (RS,NP), t_{x_{16}}=(PŁ,M)\cdot (RU,01) \cdot (US,TE) \cdot (JO,II) \cdot (OS,a) \cdot (MZ,DR) \cdot (RS,NP), t_{x_{17}}=(PŁ,M)\cdot (RU,01) \cdot (US,TE) \cdot (JO,I) \cdot (OS,a) \cdot (MZ,DR) \cdot (RS,NP), t_{x_{18}}=(PŁ,M)\cdot (RU,01) \cdot (US,TE) \cdot (JO,III) \cdot (OS,a) \cdot (MZ,DR) \cdot (RS,NP), t_{x_{19}}=(PŁ,M)\cdot (RU,99) \cdot (US,TE) \cdot (JO,I) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_{20}}=(PŁ,M)\cdot (RU,00) \cdot (US,TE) \cdot (JO,I) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_{21}}=(PŁ,K)\cdot (RU,00) \cdot (US,LO) \cdot (JO,II) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_{22}}=(PŁ,K)\cdot (RU,99) \cdot (US,LO) \cdot (JO,I) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW), t_{x_{23}}=(PŁ,M)\cdot (RU,00) \cdot (US,TE) \cdot (JO,II) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,NP), t_{x_{24}}=(PŁ,K)\cdot (RU,02) \cdot (US,LO) \cdot (JO,III) \cdot (OS,a) \cdot (MZ,DS) \cdot (RS,ZW).
Klasyfikacja Rocchia
Jako materiał na II zajęcia.
Grupowanie obiektów tą metodą rozpoczynamy wybierając za potencjalne centrum grupy obiekt x_{14} :
t_{x_{14}}=(PŁ,K)\cdot (RU,01) \cdot (US,LO) \cdot (JO,I) \cdot (OS,a) \cdot (MZ,DR) \cdot (RS,NP)
Przeprowadzając test gęstości dla wybranego centrum grupy, obliczamy współczynniki podobieństwa, określamy rangę obiektów ze zbioru X i szeregujemy obiekty względem rangi:
\begin{matrix} Obiekt & Współczynnik\ podobieństwa & Ranga\ obiektu \\ x_{14} & 1 & 1 \\ x_{13} & 1 & 2 \\ x_1 & 0.714 & 3\\ x_{17} & 0.714 & 4\\ x_5 & 0.571 & 5\\ x_6 & 0.571 & 6\\ x_{15} & 0.571 & 7\\ x_{16} & 0.571 & 8\\ x_{18} & 0.571 & 9\\ x_{22} & 0.571 & 10\\ x_2 & 0.429 & 11\\ x_9 & 0.429 & 12\\ x_{10} & 0.429 & 13\\ x_{11} & 0.429 & 14\\ x_{21} & 0.429 & 15 \\ x_{24} & 0.429 & 16 \\ x_3 & 0.286 & 17 \\ x_{19} & 0.286 & 18 \\ x_{20} & 0.286 & 19 \\ x_{23} & 0.286 & 20 \\ x_4 & 0.143 & 21 \\ x_7 & 0.143 & 22 \\ x_8 & 0.143 & 23 \\ x_{12} & 0.143 & 24 \end{matrix}
Załóżmy, że co najmniej N_2 = 6 obiektów powinno mieć współczynnik podobieństwa p_2 \geq 0.571 , a co najmniej N_1 = 12 obiektów współczynnik p_1 \geq 0.398 . Przy takich parametrach obiekt x_{14} przeszedł test gęstości, dzięki czemu otrzymaliśmy grupę o rozmiarach3o współczynnikach podobieństwa większych jak p_{min} i odpowiednio o współczynnikach nie mniejszych jak p_{min} M_1 = 10 , M_2 = 16 . Szukając p_{min} = p^* otrzymujemy:
p_{min} = 0.42857
Wynika z tego, że pierwszą grupę X_1 będą tworzyły obiekty:
X_1 = \{ x_{14}, x_{13}, x_1, x_{17}, x_5, x_6, x_{15}, x_{16}, x_{18}, x_{22}, x_2, x_9, x_{10}, x_{11}, x_{21}, x_{24} \},
a centroid będzie postaci:
C = (PŁ,K)\cdot(PŁ,M)\cdot(RU,99)\cdot(RU,00)\cdot(RU,01)\cdot(RU,02)\cdot(US,LO)\cdot(US,TE)\cdot(JO,I)\cdot(JO,II)\cdot(JO,III)\cdot(OS,a)\cdot(OS,d)\cdot(MZ,DR)\cdot(RS,NP)Kolejna iteracja algorytmu przeprowadzona dla tego centroidu doprowadzi do poprawienia grupy i otrzymania:
X_1' = \{ x_1, x_5, x_6, x_{13}, x_{14}, x_{15}, x_{16}, x_{17}, x_{18}, x_{22} \}o centroidzie:
C_1' = (PŁ,K)\cdot(PŁ,M)\cdot(RU,99)\cdot(RU,00)\cdot(RU,01)\cdot(RU,02)\cdot(US,LO)\cdot(US,TE)\cdot(JO,I)\cdot(JO,II)\cdot(JO,III)\cdot(OS,a)\cdot(OS,d)\cdot(MZ,DR)\cdot(RS,NP)Pozostałe obiekty traktujemy jako swobodne i przeprowadzamy na nich kolejne grupowania w celu wyłonienia kolejnych grup z założonymi wartościami N_1, N_2, p_1, p_2 .
“Przeskakując kilka iteracji” uzyskano następujące grupy:
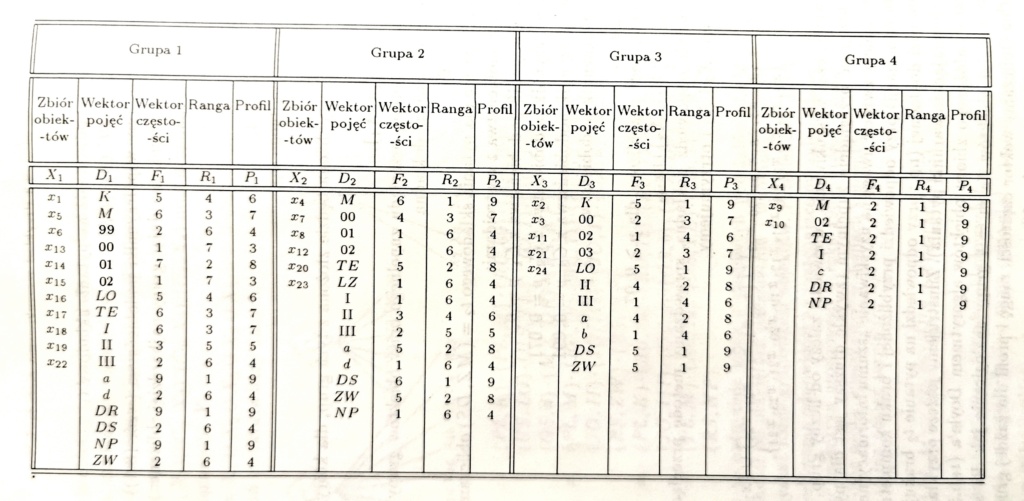
(C_1, X_1), (C_2, X_2), (C_3, X_3), (C4, X4) oraz grupę niezwiązaną X_{NZ} do której należy obiekt x_19, którego nie udało się nigdzie zgrupować.
Test koherencji powinien spełnić poniższe równanie:
X = X_1 \cup X_2 \cup X_3 \cup X_4 \cup X_{NZ}
Po powyższych przetwarzaniach nasza Baza Danych winna przybrać poniższą strukturę:
gdzie centroidy grup są:
C_1 = (PŁ,K)\cdot(PŁ,M)\cdot(RU,99)\cdot(RU,00)\cdot(RU,01)\cdot(RU,02)\cdot(US,LO)\cdot(US,TE)\cdot(JO,I)\cdot(JO,II)\cdot(JO,III)\cdot(OS,a)\cdot(OS,d)\cdot(MZ,DR)\cdot(RS,NP) \\ C_2 = (PŁ,M)\cdot(RU,00)\cdot(RU,01)\cdot(RU,02)\cdot(US,LZ)\cdot(US,TE)\cdot(JO,I)\cdot(JO,II)\cdot(JO,III)\cdot(OS,a)\cdot(OS,d)\cdot(MZ,DR)\cdot(RS,ZW)\cdot(RS,NP) \\ C_3 = (PŁ,K)\cdot(RU,00)\cdot(RU,01)\cdot(RU,02)\cdot(RU,03)\cdot(US,LO)\cdot(JO,II)\cdot(JO,III)\cdot(OS,a)\cdot(OS,b)\cdot(MZ,DS)\cdot(RS,ZW) \\ C_4 = (PŁ,M)\cdot(RU,02)\cdot(US,TE)\cdot(JO,I)\cdot(OS,c)\cdot(MZ,DR)\cdot(RS,NP)Takie grupowanie jest konsekwencją przybranych parametrów i wybranego centroidu grupy.
Zadanie pytania do systemu
Przykładowe pytanie do systemu może mieć postać: Podaj mężczyzn urodzonych w 1999r, którzy ukończyli liceum zawodowe oraz osoby mieszkające w domach studenta. Standaryzując pytanie do termu przybiera ono postać:
t = (PŁ,M)\cdot(RU,99)\cdot(US,LZ) + (MZ,DS)
widać, że pytanie jest sumą termów składowych t = t_1 + t_2 , czyli odpowiedź będzie sumą odpowiedzi na termy składowe: \sigma(t) = \sigma(t_1) \cup \sigma(t_2).
Szukając odpowiedzi, znajdźmy odpowiedź na t_1 = (PŁ,M)\cdot(RU,99)\cdot(US,LZ).
W tym celu obliczamy według wzoru [1] współczynniki podobieństwa termu t_1 z wszystkimi centroidami, szukając najbardziej zbliżonych grup:
- dla C_1 \qquad p=0.133,
- dla C_2 \qquad p=0.143,
- dla C_3 \qquad p=0.0,
- dla C_4 \qquad p=0.143,
- dla NZ (x_{19}) \qquad t_1 \nleq t_{x_{19}}
Odpowiedź najbardziej zbliżona będzie dla grup z p \geq 0.14, czyli \sigma(t_1) =\{ X_2 \cup X_4 \}. Następnie dokonując przeglądu zupełnego tych grup znajdujemy odpowiedź dokładną, w tym przypadku: \sigma(t_1) = \{ \varnothing \}
Analogicznie powtarzając algorytm dla drugiego termu składowego t_2=(MZ,DS) obliczamy podobieństwa:
- dla C_1 \qquad p=0.0,
- dla C_2 \qquad p=0.071,
- dla C_3 \qquad p=0.091,
- dla C_4 \qquad p=0.0,
- dla NZ (x_{19}) \qquad t_1 \leq t_{x_{19}}
i określamy odpowiedź zbliżoną dla p \geq 0.07 otrzymując \sigma(t_2) = \{X_2 \cup X_3 \} \cup x_{19}. Implikuje to konieczność dokonania przeglądu zupełnego w X_2 i X_3 otrzymując:
\sigma(t_2) = \{ x_4, x_7, x_8, x_{12}, x_{20}, x_{23} \} \cup \{ x_2, x_3, x_{11}, x_{21}, x_{24} \} \cup x_{19} , co daje:
\sigma(t_2) = \{ x_2, x_3, x_4, x_7, x_8, x_{11}, x_{12}, x_{19}, x_{20}, x_{21}, x_{23}, x_{24} \}
Należy zwrócić uwagę na “szum informacyjny” w postaci nadmiarowej informacji przy odpowiedzi przybliżonej, oraz niekompletność wyszukiwania – brakuje obiektu x_{22} , który spełnia warunki wyszukiwania.
Klasyfikacja Doyle’a
Jako materiał na III zajęcia.
Za literaturowym przykładem przyjmujemy podział bazy na 4 grupy (m = 4). Obliczamy wektor częstości, rangę i profil dla każdej grupy. Przyjmujemy wartość bazową b=10.
P_j = (b - R_j) dla każdego deskryptora d_i .
Obliczamy funkcję punktującą g(x_i, P_j) dla każdego obiektu x_i. Funkcja punktująca jest sumą wartości pozycyjnych profili dla wszystkich deskryptorów występujących w opisie danego obiektu. Wszystkie deskryptory należące do opisu obiektu mogą wystąpić w kilku grupach (profilach). Niezależnie od wstępnego zaklasyfikowania obiektu należy wybrać profil, w której wartość funkcji punktującej jest największa.
| Obiekt x_i | Profil P_j | Funkcja punktująca g(x_i, P_j) |
| x_1 | 1 | 46 |
| x_5 | 1 | 48 |
| x_6 | 1 | 48 |
| x_{13} | 1 | 54 |
| x_{14} | 1 | 54 |
| x_{15} | 1 | 51 |
| x_{16} | 1 | 54 |
| x_{17} | 1 | 56 |
| x_{18} | 1 | 53 |
| x_{19} | 1 | 42 |
| x_{22} | 1 | 40 |
| x_{4} | 2 | 51 |
| x_{7} | 2 | 55 |
| x_{8} | 2 | 48 |
| x_{12} | 2 | 50 |
| x_{20} | 2 | 53 |
| x_{23} | 2 | 51 |
| x_{2} | 3 | 59 |
| x_{3} | 3 | 57 |
| x_{11} | 3 | 59 |
| x_{21} | 3 | 59 |
| x_{24} | 3 | 56 |
| x_{9} | 4 | 63 |
| x_{10} | 4 | 63 |
Zgodnie z tezą, że deskryptory należące do opisu obiektu mogą należeć do różnych profili powoduje to konieczność wybrania tych, które mają największą wartość funkcji punktującej, tak więc obiekty:
\left. \begin{matrix} g(x_4,P_1)=38 & g(x_4,P_2)=55 \\ g(x_7,P_1)=33 & g(x_7,P_2)=55 \\ g(x_8,P_1)=39 & g(x_8,P_2)=48 \\ g(x_{20},P_1)=41 & g(x_{20},P_2)=53 \\ g(x_{23},P_1)=44 & g(x_{23},P_2)=51 \\ \end{matrix} \right \} \Rightarrow P_2 \\ \left. \begin{matrix} g(x_{11},P_1)=37 & g(x_{11},P_3)=59 \\ g(x_{24},P_1)=36 & g(x_{24},P_3)=56 \\ \end{matrix} \right \} \Rightarrow P_3
W drugiej fazie ponownie grupujemy zgodnie ze wzorem:
X_j' = \{ x_i, g(x_i, P_j) \geq T_j \}
gdzie: \qquad T_j = \left \{\begin{matrix} H_j' = \alpha(H_j'-T), & dla & H_j'>T \\ T, & dla & H_j' \leq T \end{matrix} \right.
Dla grupy 1 przyjmujemy:
- T = 40 – założona wartość progowa funkcji punktującej dla j-tej grupy,
- H_1 = Max g(x_i, P_j) = 56 – maksymalna wartość funkcji punktującej w j-tej grupie,
- \alpha = 0,5 – założony współczynnik z zakresu 0 \leq \alpha \leq 1,
- T_1=56-0,5*(56-40) = 48,
czyli grupa 1
X_1'=\{x_i, g(x_i, P_1) \geq 48 \} \Rightarrow X_1'= \{ x_5, x_6, x_{13}, x_{14}, x_{15}, x_{17}, x_{18} \}Dla grupy 2 przyjmujemy:
- T = 40 ,
- H_2 = Max g(x_i, P_j) = 55 ,
- \alpha = 0,5,
- T_2=55-0,5*(55-40) = 47,5,
czyli grupa 2
X_2'=\{x_i, g(x_i, P_2) \geq 47,5 \} \Rightarrow X_2'= \{ x_4, x_7, x_{8}, x_{12}, x_{20}, x_{23} \}Dla grupy 3 przyjmujemy:
- T = 50 ,
- H_3 = Max g(x_i, P_j) = 59 ,
- \alpha = 0,5,
- T_3=59-0,5*(59-50) = 54,5,
czyli grupa 3
X_3'=\{x_i, g(x_i, P_3) \geq 54,5 \} \Rightarrow X_3'= \{ x_2, x_3, x_{11}, x_{21}, x_{24} \}Dla grupy 4 przyjmujemy:
- T = 63 ,
- H_4 = Max g(x_i, P_j) = 63 ,
- \alpha = 0,5,
- T_4=63-0,5*(63-63) = 63,
czyli grupa 4
X_4'=\{x_i, g(x_i, P_3) \geq 63 \} \Rightarrow X_4'= \{ x_9, x_{10} \}.
W ten sposób doprowadziliśmy do powstania m + 1 grup, gdyż pozostała grupa 5 – obiektów nie związanych.
Grupa 5
X_5'= \{ x_1, x_{19}, x_{22} \}.
Dalsze iteracje nie zmieniają grup, co znaczy, że w bazie danych mamy wydzielonych 5 grup.
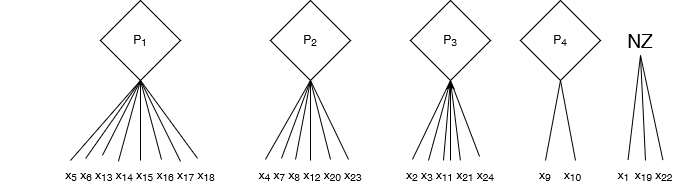
Uzyskane wektory pojęć są następujące:
Dla profilu P_1
Wektor pojęć D_1 = (PŁ,K)\cdot(PŁ,M)\cdot(RU,00)\cdot(RU,01)\cdot(RU,02)\cdot(US,LO)\cdot(US,TE)\cdot(JO,I)\cdot(JO,II)\cdot(JO,III)\cdot(OS,a)\cdot(OS,d)\cdot(MZ,DR)\cdot(RS,NP),
Zbiór obiektów: X_1 = \{ x_{5}, x_{6}, x_{13}, x_{14}, x_{15}, x_{16}, x_{17}, x_{18} \}
Dla profilu P_2
Wektor pojęć D_2 = (PŁ,M)\cdot(RU,00)\cdot(RU,01)\cdot(RU,02)\cdot(US,TE)\cdot(US,LZ)\cdot(JO,I)\cdot(JO,II)\cdot(JO,III)\cdot(OS,a)\cdot(OS,d)\cdot(MZ,DS)\cdot(RS,ZW)\cdot(RS,NP),
Zbiór obiektów: X_2 = \{ x_{4}, x_{7}, x_{8}, x_{12}, x_{20}, x_{23} \}
Dla profilu P_3
Wektor pojęć D_3 = (PŁ,K)\cdot(RU,00)\cdot(RU,02)\cdot(RU,03)\cdot(US,LO)\cdot(JO,II)\cdot(JO,III)\cdot(OS,a)\cdot(OS,B)\cdot(MZ,DS)\cdot(RS,ZW),
Zbiór obiektów: X_3 = \{ x_{2}, x_{3}, x_{11}, x_{21}, x_{24} \}
Dla profilu P_4
Wektor pojęć D_4 = (PŁ,M)\cdot(RU,02)\cdot(US,TE)\cdot(JO,I)\cdot(OS,c)\cdot(MZ,DR)\cdot(RS,NP),
Zbiór obiektów: X_4 = \{ x_{9}, x_{10} \}
Grupa 5: NZ (obiekty niezwiązane – swobodne)
t_{x_{1}} = (PŁ,K)\cdot(RU,01)\cdot(US,LO)\cdot(JO,III)\cdot(OS,d)\cdot(MZ,DR)\cdot(RS,NP)
t_{x_{19}} = (PŁ,M)\cdot(RU,99)\cdot(US,TE)\cdot(JO,I)\cdot(OS,a)\cdot(MZ,DS)\cdot(RS,ZW)
t_{x_{22}} = (PŁ,K)\cdot(RU,99)\cdot(US,LO)\cdot(JO,I)\cdot(OS,a)\cdot(MZ,DS)\cdot(RS,ZW)
Zadanie pytania do systemu
Pytanie w postaci termu:
t = (PŁ,M)\cdot(RU,99)\cdot(US,LZ) + (MZ,DS), czyli t = t_1 + t_2
\sigma(t) = \sigma(t_1) \cup \sigma(t_2)Dla termu t_1:
\sigma(t_1) = \sigma((PŁ,M)\cdot(RU,99)\cdot(US,LZ))Porównując deskryptory pytania z wektorami pojęć grup, selekcjonujemy grupy dające przybliżoną odpowiedź na pytanie pierwsze. Jednak żaden profil nie zawiera wszystkich niezbędnych deskryptorów pytania, to na końcu porównujemy jeszcze ze zbiorem NZ.
Otrzymujemy: \sigma(t_1)= \{ \varnothing \}.
Dla termu t_2:
\sigma(t_2) = \sigma((MZ,DS)).
Poprzez analogię, selekcjonujemy grupy zawierające w wektorach pojęć szukane deskryptory i uzyskujemy odpowiedź przybliżoną:
\sigma(t_2) \approx \{X_2 \cup X_3 \}.
Dokonujemy przeglądu zupełnego w ten sposób wskazanych 14 obiektów w grupach X_2 (6\ obiektów), X_3 (5\ obiektów), oraz NZ (3\ obiekty) znajdując odpowiedź dokładną.
\sigma(t_2) = \{ x_4, x_7, x_8, x_{12}, x_{20}, x_{23} \} \cup \{ x_{2}, x_{3}, x_{11}, x_{21}, x_{24} \} \cup \{ x_{19}, x_{22} \}co daje nam w rezultacie:
\sigma(t_2) = \{ x_2, x_3, x_4, x_{7}, x_{8}, x_{11}, x_{12}, x_{19}, x_{20}, x_{21}, x_{22}, x_{23}, x_{24} \}Teoretycznie uzyskaliśmy skrócenie wyszukiwania, gdyż musieliśmy przejrzeć opisy 14 obiektów zamiast 24 w metodzie list prostych. Można zauważyć, że im szczegółowsze pytanie, tym szybsza i bardziej precyzyjna odpowiedź.
Modyfikacje metody Saltona
Modyfikacje metody to przede wszystkim zmiany wynikające z innych metod klasyfikacyjnych dla utworzenia grup. Inną kategorią jest wyszukiwanie sekwencyjne, które polega na zmodyfikowanej metodzie przeglądu zupełnego, w której po obliczeniu współczynników podobieństwa pytania z każdym opisem obiektu w bazie danych, wybieramy odpowiedź jako zbiór obiektów o najwyższych współczynnikach podobieństwa p_j .
Odpowiedź na pytanie składowe t w tym przypadku wygląda następująco:
\sigma(t_i) = \{ x_i \in X, \quad t_i \underset{p_j}\leq t_{x_i} \}
Parametry metody Saltona
Struktura bazy danych w metodzie Saltona jest skomplikowana i wymaga klasyfikacji obiektów przypisując je do grup. Wynika z tego, że proces aktualizacji jest również skomplikowany i wymaga przeprowadzenia ponownego wiązania obiektów w grupy po każdorazowej zmianie opisu obiektu. Częściowo można zagadnienie uprościć dodając nowo stworzony obiekt do grupy niezwiązanych obiektów pozostających po klasyfikacji. Jednakże zwiększanie liczebności tej grupy wpływa negatywnie na czas wyszukiwania \tau = \tau_\omega + \tau_p , gdzie \tau_\omega – czas wyboru centroidów, \tau_p – czas obliczania współczynników podobieństwa z obiektami wybranej grupy.